Формула суммы является важным математическим инструментом для вычисления итогового значения последовательности чисел. Рассмотрим основные виды формул суммирования и их применение.

Содержание

Основные формулы суммирования

Арифметическая прогрессияSn = n/2 × (a1 + an)
Геометрическая прогрессияSn = a1 × (1 - rn)/(1 - r)
Сумма натуральных чиселSn = n(n+1)/2
Сумма квадратовSn = n(n+1)(2n+1)/6

Применение формулы суммы арифметической прогрессии

Пошаговая инструкция

  1. Определите первый член прогрессии (a1)
  2. Найдите последний член прогрессии (an)
  3. Подсчитайте количество членов (n)
  4. Подставьте значения в формулу Sn = n/2 × (a1 + an)
  5. Выполните вычисления

Пример расчета

Дано:1, 4, 7, 10, 13
a1:1
an:13
n:5
Решение:S5 = 5/2 × (1 + 13) = 35

Использование формулы суммы в Excel

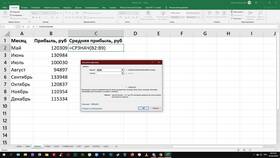
  • Функция СУММ(): =СУММ(A1:A10)
  • Суммирование с условием: =СУММЕСЛИ()
  • Множественное суммирование: =СУММПРОИЗВ()
  • Автосумма: выделите диапазон и нажмите Alt+=

Практическое применение формул суммы

ФинансыРасчет общего дохода за период
СтатистикаВычисление совокупных показателей
ФизикаСуммирование сил или энергий
ПрограммированиеАлгоритмы накопления значений

Частые ошибки при использовании

  • Неправильное определение количества членов
  • Ошибки в определении первого и последнего элемента
  • Неучет знаменателя в геометрической прогрессии
  • Неправильная расстановка скобок в формулах

Формулы суммы являются мощным инструментом для решения широкого круга задач. Правильное понимание и применение этих формул значительно упрощает математические вычисления в различных областях деятельности.

Запомните, а то забудете

Не забудьте ознакомиться со статьей: «Как найти поддержку на портале Госуслуги», это может пригодиться вам в будущем. Ещё больше полезных статей по схожей тематике вы сможете найти ниже.

— редакция сайта intimwears.ru

Другие статьи

Как называется доход самозанятого и прочее