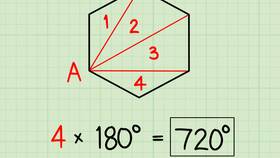
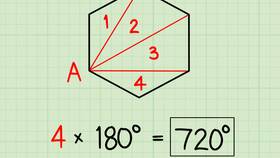
Сумма внутренних углов треугольника является одной из фундаментальных теорем евклидовой геометрии. Это свойство остается неизменным для всех типов треугольников на плоскости.
Содержание
Основная теорема
Сумма внутренних углов любого треугольника равна 180 градусам. Это можно выразить формулой:
∠A + ∠B + ∠C = 180°
Доказательство теоремы
Способ 1: Через параллельные прямые
- Проведем через вершину C прямую, параллельную стороне AB
- Углы при точке C образуют развернутый угол (180°)
- Соответственные углы равны: ∠A = ∠1, ∠B = ∠2
- Следовательно, ∠A + ∠B + ∠C = 180°
Способ 2: Практический метод
- Вырежьте треугольник из бумаги
- Оторвите все три угла
- Сложите их вместе - они образуют прямую линию (180°)
Примеры для разных типов треугольников
| Тип треугольника | Пример углов | Сумма |
| Равносторонний | 60° + 60° + 60° | 180° |
| Прямоугольный | 90° + 45° + 45° | 180° |
| Тупоугольный | 120° + 30° + 30° | 180° |
Следствия из теоремы
- В треугольнике не может быть двух прямых или тупых углов
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним
- Сумма острых углов прямоугольного треугольника равна 90°
Решение задач
В треугольнике ABC известны два угла: ∠A = 45°, ∠B = 60°. Найдите ∠C.
Решение:
∠C = 180° - (45° + 60°) = 180° - 105° = 75°
Исключения и особые случаи
Сферические треугольники
На сфере сумма углов треугольника всегда превышает 180° и может достигать 540°.
Гиперболические треугольники
В гиперболической геометрии сумма углов треугольника всегда меньше 180°.
Практическое применение
- Архитектура и строительство
- Геодезия и картография
- Компьютерная графика
- Навигация и астрономия
Историческая справка
Это свойство треугольников было известно еще древнегреческим математикам. Евклид использовал его как основу для многих доказательств в своих "Началах".