Сумма внутренних углов любого четырехугольника составляет 360 градусов. Это фундаментальное свойство евклидовой геометрии, которое справедливо для всех простых четырехугольников, независимо от их формы.
Содержание
Доказательство теоремы о сумме углов
Существует два основных способа доказать, что сумма углов четырехугольника равна 360°:
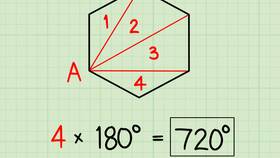
Метод разбиения на треугольники
- Провести диагональ в четырехугольнике, разделяющую его на два треугольника
- Сумма углов каждого треугольника равна 180°
- Два треугольника дают: 180° × 2 = 360°
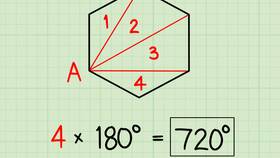
Общий метод для n-угольников
- Формула суммы углов n-угольника: (n-2) × 180°
- Для четырехугольника (n=4): (4-2) × 180° = 2 × 180° = 360°
Примеры для различных типов четырехугольников
| Тип четырехугольника | Сумма углов |
| Прямоугольник | 90° + 90° + 90° + 90° = 360° |
| Ромб | α + α + (180°-α) + (180°-α) = 360° |
| Трапеция | α + β + (180°-α) + (180°-β) = 360° |
| Произвольный выпуклый четырехугольник | A + B + C + D = 360° |
Практическое применение свойства
Знание суммы углов четырехугольника используется:
- В геометрических расчетах и построениях
- При решении задач на нахождение неизвестных углов
- В архитектуре и строительстве
- В компьютерной графике и 3D-моделировании
Важное замечание
Для невыпуклых четырехугольников сумма углов также равна 360°, но метод вычисления может отличаться. В случае самопересекающихся четырехугольников это правило не применяется.
Понимание этого свойства помогает решать широкий круг геометрических задач и является базовым знанием в курсе планиметрии.